How to estimate the total number of Nazi Tanks?

Historical Context

During World War II, Allied intelligence faced the challenge of estimating German tank production. This led to the development of statistical methods that significantly outperformed traditional intelligence gathering.

Here's how the simulation works:

1. We have a secret number of tanks (500 in this case).
2. We pretend to "capture" 5 tanks and look at their serial numbers.
3. Based on these 5 numbers, we try to guess the total number of tanks.
4. We repeat this process 1000 times to see how good our guessing methods are.

Here's the strategy:

• The "Simple" method (MLE): We just use the highest number we see.
• The "Smart" method (Unbiased): We use a slightly more complicated calculation that tries to account for the tanks we didn't see.

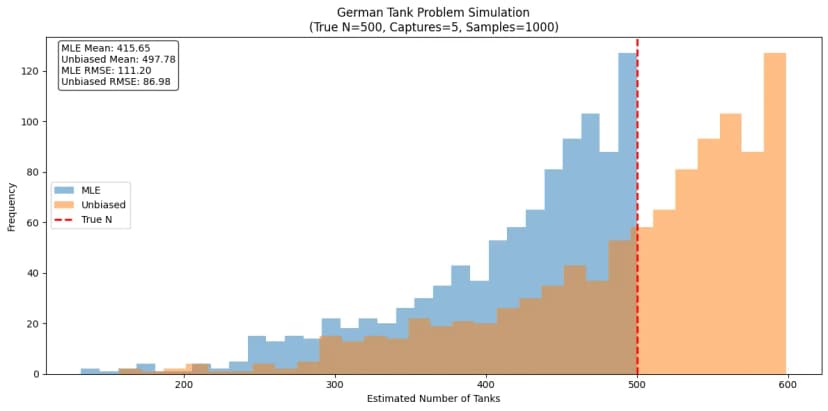
Observations:

1. The "Simple" method (blue) tends to guess too low. Its average guess is about 416 tanks, which is less than the real 500.
2. The "Smart" method (orange) does better. Its average guess is about 498 tanks, very close to the real 500!
3. But notice how the orange bars are more spread out. This means the "Smart" method can sometimes be way off, even though it's better on average.
4. The "Simple" method is more consistent (the blue bars are more bunched together), but it's consistently too low.

Estimation Methodology

1. Basic Maximum Likelihood Estimator

The simplest approach uses the maximum observed serial number (m) as an estimator:

N̂ = m

While simple, this estimator is biased low, as P(N̂ ≤ N) = 1.

Improved Estimators

Sample Maximum Plus Average Gap

A more sophisticated estimator adds the average gap between observed serial numbers:

N̂ = m + (m - k) / k

Where:

• m: maximum observed serial number
• k: number of observed samples

This can be interpreted as the maximum plus the average gap, providing a less biased estimate.

Derivation from Order Statistics

The estimator can be derived from order statistics. For a sample of size k from a uniform discrete distribution on {1, ..., N}:

E[m] = N * k / (k + 1)

Solving for N yields the unbiased estimator:

N̂ = m * (k + 1) / k - 1

Probability Analysis

The probability of observing a specific set of serial numbers {s₁, ..., sₖ} given N tanks is:

P({s₁, ..., sₖ} | N) = k! / (N * (N-1) * ... * (N-k+1))

Maximizing this probability (or its logarithm) with respect to N yields the maximum likelihood estimator.